Το μαθηματικό μοντέλο πρόβλεψης μιας πανδημίας
Σύνταξη άρθρου: Ευθύμης Κυρίκος
Επιμέλεια άρθρου: Κωνσταντίνος Ουρανός

Όλα τα οικοσυστήματα στη Γη εξελίχθηκαν με το πέρασμα του χρόνου δημιουργώντας μια τεράστια βιοποικιλότητα στον πλανήτη. Η διαδικασία αυτή δεν θα μπορούσε να πραγματοποιηθεί, αν δεν υπήρχαν μηχανισμοί διατήρησης της πληθυσμιακής ισορροπίας. Η διατήρηση του αριθμού των ατόμων σε ένα οικοσύστημα είναι εξέχουσας σημασίας καθώς η έλλειψή της δημιουργεί προβλήματα τόσο σε είδη που κινδυνεύουν με εξαφάνιση όσο και σε αυτά που τελικά κυριαρχούν. Ας δούμε όμως ποια μαθηματικά μοντέλα καταγραφής και κατανόησης της αύξησης του πληθυσμού έχουν προταθεί στον διάβα του χρόνου.
Το μοντέλο της εκθετικής αύξησης
Ένα από τα πρώτα μοντέλα που χρησιμοποιήθηκαν για την περιγραφή της ανάπτυξης ενός πληθυσμού, είναι το εκθετικό μοντέλο. Βάσει του μοντέλου αυτού, αν ο αρχικός πληθυσμός ενός είδους στο οικοσύστημα είναι Xo άτομα, τότε στην επόμενη γενιά θα είναι X1=ρΧο. Το μοντέλο περιγράφεται από τη γενική εξίσωση: Xv=ρΧv-1 όπου το v είναι ο ρυθμός αναπαραγωγής του είδους και η γενιά.
Αν για παράδειγμα σε ένα οικοσύστημα ο πληθυσμός ενός είδους, λόγου χάρη ο πληθυσμός των κουνελιών, είναι αρχικά 10 άτομα (Xo = 10) και ο ρυθμός αναπαραγωγής είναι ίσος με ρ=2, τότε η επόμενη γενιά θα έχει πληθυσμό Χ1 = 2·Χο = 20 δηλαδή θα υπάρχει διπλασιασμός του πληθυσμού. Αντίστοιχα οι επόμενες γενιές θα έχουν πληθυσμό Χ2 = 40, Χ3 = 80 , Χ4 = 160 και ούτω καθεξής.
Παρατηρείται πως μέσω αυτού του μοντέλου ο πληθυσμός ενός είδους αυξάνεται συνεχώς. Γενικά για ρυθμό ανάπτυξης ρ > 1 υπάρχει αύξηση του πληθυσμού, ενώ για ρυθμό ρ < 1 υπάρχει μείωση του πληθυσμού. Το παραπάνω μοντέλο ωστόσο αγνοεί ένα βασικό δομικό πρόβλημα της φύσης. Βάσει του παραπάνω παραδείγματος βλέπουμε πως μέσα σε 5 γενιές ο πληθυσμός των κουνελιών αυξήθηκε 16 φορές, το οποίο σαν φαινόμενο δεν συμβαίνει ιδιαίτερα συχνά στη φύση. Η συμπεριφορά αυτή «παρουσιάζεται», γιατί δε λαμβάνονται υπόψη οι περιορισμοί που θέτει το ίδιο το περιβάλλον στην ανάπτυξη του κάθε είδους.
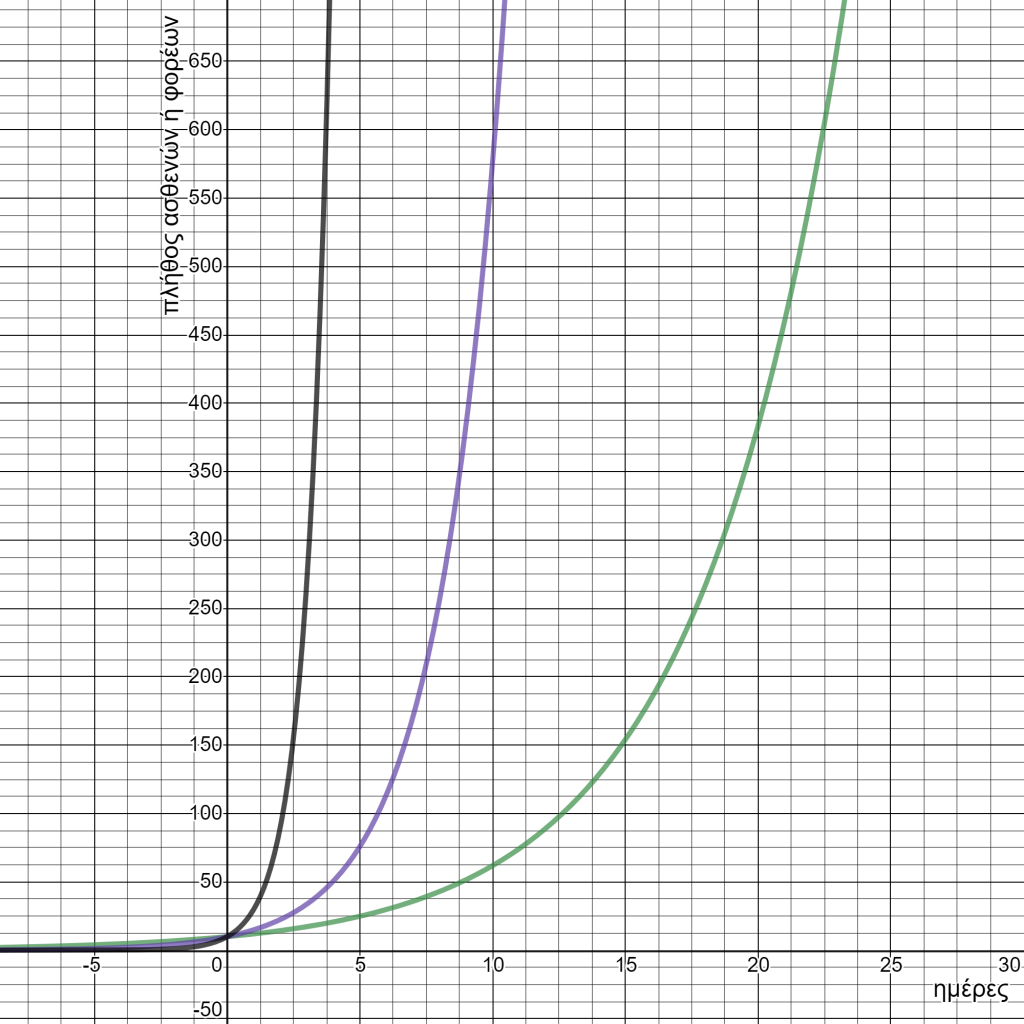
Ανάπτυξη με περιορισμούς
Το 1836 ο Βέλγος μαθηματικός Πιερ Φρανσουά Βερχούλστ (Pierre François Verhulst) πρότεινε μια ορθότερη μέθοδο περιγραφής της εξέλιξης των πληθυσμών, την «Ανάπτυξη με περιορισμούς» μέσω ενός μαθηματικού μοντέλου που ονομάζεται «Λογιστικό μοντέλο». Σε αυτό το πρόβλημα εισάγεται ο περιορισμός του μέγιστου πληθυσμού, δηλαδή το γεγονός πως το οικοσύστημα δεν μπορεί να διατηρήσει έναν πληθυσμό πέρα από ένα συγκεκριμένο αριθμό, λόγω περιορισμένων πόρων. Ας σκεφτούμε πως σε ένα οικοσύστημα ο αριθμός των κουνελιών αυξάνεται εκθετικά. Μέσα σε μερικές γενιές ο πληθυσμός θα έχει αυξηθεί σε τέτοιο βαθμό, που δεν θα μπορεί να βρει τροφή ή καθαρό νερό καθώς θα καταναλώνει περισσότερο από όσο το οικοσύστημα μπορεί να παραγάγει. Έτσι ο πληθυσμός θα αρχίσει να μειώνεται.
Το λογιστικό μοντέλο ανάπτυξης περιγράφεται από την εξίσωση:
![]()
Ο ρυθμός αύξησης του πληθυσμού από γενιά σε γενιά υπολογίζεται από τον εξής τύπο:
![]()
Όπου Ν(to) ο αρχικός πληθυσμός, N(t1) ο πληθυσμός μετά την πρώτη γενιά, ρ ο ρυθμός αναπαραγωγής του πληθυσμού και Κ ο μέγιστος πληθυσμός που μπορεί να υποστηρίξει το οικοσύστημα. Γραφικά η συμπεριφορά ενός πληθυσμού στο μοντέλο έχει την εξής συμπεριφορά:
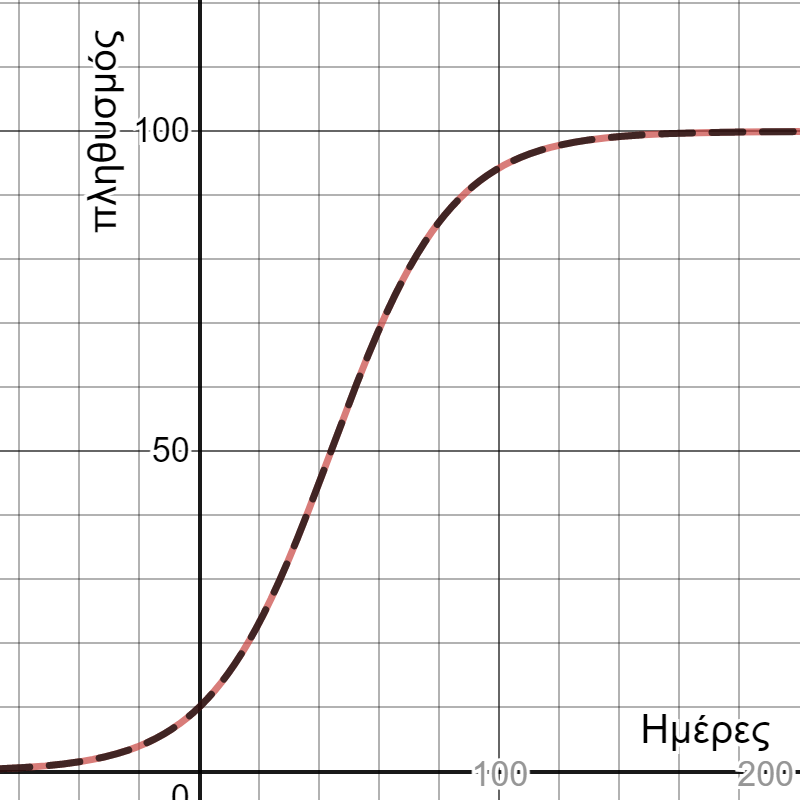
Στην παραπάνω σχέση εισάγεται ακόμα ένας όρος που περιγράφει τον μέγιστο πληθυσμό του οικοσυστήματος. Πράγματι, όσο ο ενεργός πληθυσμός Ν(t) πλησιάζει το μέγιστο K τότε ο ρυθμός ανάπτυξης πλησιάζει το μηδέν και έχουμε ισορροπία πληθυσμών στο οικοσύστημα. Από το διάγραμμα φαίνεται πως, μετά από ένα ορισμένο χρονικό διάστημα, ο πληθυσμός τελικά ισορροπεί σε έναν τελικό αριθμό.
Σύστημα ελέγχου πληθυσμού
Σήμερα χρησιμοποιούνται πολλά συστήματα για τον έλεγχο πληθυσμών μικροοργανισμών κυρίως στη βιομηχανία τροφίμων. Μια από τις κλασσικότερες διεργασίες είναι η παστερίωση του γάλακτος όπου μέσω ελέγχου της θερμοκρασίας του γάλακτος γίνεται μείωση του πληθυσμού των επιβλαβών μικροοργανισμών ώστε να καταστεί το γάλα κατάλληλο για κατανάλωση.
Κάθε διεργασία ελέγχου περιγράφεται από ένα σύστημα εξισώσεων που ονομάζεται «Φυσικό μοντέλο συστήματος». Τα συστήματα αυτά περιγράφουν με μαθηματικό τρόπο τη συμπεριφορά μιας διεργασίας με την πάροδο του χρόνου (χρονικά αναλλοίωτα συστήματα). Συνήθως τα συστήματα αυτά είναι ιδιαίτερα πολύπλοκα για να περιγράψουν με τη μέγιστη ακρίβεια την πραγματικότητα. Ωστόσο στις περισσότερες εφαρμογές έχουν βρεθεί είτε εμπειρικά, είτε με διάφορες αναλυτικές και αριθμητικές μεθόδους απλοποιημένα συστήματα ώστε να είναι εύκολη η μελέτη και ο έλεγχος των διεργασιών. Ένα διάγραμμα μιας τέτοιας διεργασίας είναι το ακόλουθο:
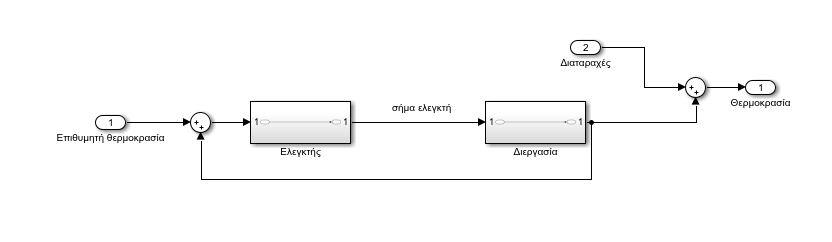
Για να μπορέσουμε να διατηρήσουμε υπό έλεγχο μια διεργασία χρησιμοποιούμε τεχνητά μέσα τους «ελεγκτές». Για παράδειγμα, στην περίπτωση της παστερίωσης το φυσικό μας σύστημα είναι ένα δοχείο γεμάτο με γάλα το οποίο και θα πρέπει να παστεριωθεί. Για να παστεριώσουμε το γάλα χωρίς να καεί και να καταστραφεί θα πρέπει να γίνεται έλεγχος της θερμοκρασίας του μέσα στο δοχείο. Ο ελεγκτής αυτής της διεργασίας θα πρέπει να λαμβάνει τη θερμοκρασία του γάλακτος, να τη συγκρίνει με την επιθυμητή και να αλλάζει τη θερμότητα που προσφέρει στο δοχείο, είτε επενεργώντας σε ένα σύστημα ελέγχου παροχής ατμού είτε με ηλεκτρικό τρόπο, προσφέροντας περισσότερη ή λιγότερη θερμότητα στο δοχείο ανάλογα με τη θερμοκρασία μέσα σε αυτό.
Η παραπάνω διεργασία αποτελεί έμμεσα έναν τρόπο ελέγχου ενός πληθυσμού μικροοργανισμών μέσα σε ένα δοχείο. Η διεργασία ελέγχει πόσοι μικροοργανισμοί πεθαίνουν ελέγχοντας τη θερμοκρασία του περιβάλλοντός τους. Φαινομενικά είναι ένα απλό παράδειγμα, ωστόσο μια παρόμοια λογική μπορεί να εφαρμοστεί σε όλα τα αντίστοιχα συστήματα. Ας τη δούμε.
Δυναμικό μοντέλο επιδημιών
Από το 1927 – 1933 ο ιατρός Άντερσον Γκρέι Μάκεντρικ (A.G. McKendrick) και ο βιοχημικός Ουίλλιαμ Όγκιλβυ Κέρμακ (William Ogilvy Kermack) ανέπτυξαν ένα διαμερισματικό μοντέλο, που περιγράφει την εξέλιξη μιας πανδημίας (Μοντέλο SIR). Σύμφωνα με το μοντέλο αυτό ο πληθυσμός χωρίζεται σε τρεις μεγάλες ομάδες:
- Δυνητικά ασθενείς (Susceptible).
- Ασθενείς και φορείς (Infected).
- Θεραπευθέντες (Recovered).
Αρχικά όλος ο πληθυσμός αποτελείται από δυνητικά ασθενείς, αφού δεν έχει εμφανιστεί η επιδημία και δεν έχει νοσήσει κανείς ακόμα. Μόλις εμφανιστεί το πρώτο μολυσμένο άτομο, χωρίς να έχει εμφανίσει ακόμα συμπτώματα, έρχεται σε επαφή με άλλους και διαδίδει την επιδημία. Σε αυτήν τη φάση έχουμε μεταφορά πληθυσμού από την ομάδα των δυνητικά ασθενών στην ομάδα των ασθενών ή φορέων. Στη συνέχεια οι ασθενείς γίνονται καλά, αποκτούν ανοσία και κατηγοριοποιούνται στην ομάδα των θεραπευθέντων. Μαθηματικά το παραπάνω μοντέλο περιγράφεται από τις ακόλουθες εξισώσεις:
![]()
![]()
όπου S(t) το πλήθος των δυνητικά φορέων τη χρονική στιγμή t, I(t) το πλήθος των ασθενών ή φορέων τη χρονική στιγμή t, R(t) το πλήθος των θεραπευθέντων τη χρονική στιγμή t, β το ποσοστό αυτών που ασθενούν ανά μονάδα χρόνου (π.χ., ανά ημέρα), γ το ποσοστό αυτών που θεραπεύονται ανά μονάδα χρόνου (π.χ., ανά ημέρα) και Π = S(t) + I(t) + R(t) το σύνολο του πληθυσμού.
Μοντέλο ελέγχου της επιδημίας
Σήμερα, λόγω της κατάστασης, που επικρατεί παγκοσμίως, είναι απαραίτητος ο έλεγχος του πληθυσμού του ιού Sars-Cov-2 στον άνθρωπο. Όπως αναφέρθηκε παραπάνω, ο ιός, όπως όλοι οι οργανισμοί, ακολουθεί το λογαριθμικό μοντέλο ανάπτυξης. Το λογαριθμικό μοντέλο ωστόσο παρουσιάζει μια ιδιομορφία. Αν ο μέγιστος πληθυσμός ενός είδους σε ένα οικοσύστημα είναι πολύ μεγάλος, τότε η ανάπτυξη του πληθυσμού στα αρχικά της στάδια συμπεριφέρεται παρόμοια με το εκθετικό μοντέλο, που, όπως είδαμε, αυξάνει ραγδαία και σε πολύ μικρό χρονικό διάστημα τον πληθυσμό των νοσούντων.
![]()
Με δεδομένο πως υπάρχουν περίπου 7,5 δισεκατομμύρια άνθρωποι στον πλανήτη, ο αριθμός είναι ένα τεράστιο νούμερο. Έτσι το κλάσμα N(to)/K για τεράστιο αριθμό του K είναι πολύ κοντά στο μηδέν. Έτσι η παραπάνω σχέση μπορεί να απλοποιηθεί σε αυτήν του εκθετικού μοντέλου χωρίς περιορισμό δηλαδή N(t1) = ρ·N(to).
Σε πρακτικό επίπεδο στα αρχικά στάδια εξάπλωσης μιας επιδημίας δεν υφίστανται οι περιορισμοί του περιβάλλοντος καθώς ο πληθυσμός των ασθενών είναι πολύ μικρός ενώ των δυνητικά ασθενών είναι πολύ μεγάλος.
Το παραπάνω φαινόμενο είναι ιδιαίτερα σημαντικό για τον έλεγχο των επιδημιών και απαιτεί άμεση προσοχή. Για να δώσουμε ένα παράδειγμα, στην περίπτωση του SARS-Cov-2 όπου ο ρυθμός μετάδοσης είναι κοντά στο τρία, αν δεν υπάρξει καμία προσπάθεια περιορισμού, τότε αυτό σημαίνει πως καθημερινά θα τριπλασιάζονται οι νέοι ασθενείς και φορείς κατά την αρχική φάση εξάπλωσης. Για να γίνει πιο αντιληπτό, αν την πρώτη ημέρα υπάρχουν μόλις 10 ασθενείς, μετά από 10 ημέρες ο αριθμός τους θα έχει φτάσει τα 10.485.760 δηλαδή περισσότεροι από τον πληθυσμό της Ελλάδας! Φυσικά κάτι τέτοιο δεν μπορεί να συμβεί καθώς οι περισσότεροι άνθρωποι κυκλοφορούν σε περιορισμένο χώρο και συναθροίζονται με λίγους ανθρώπους, οπότε και ο δείκτης μετάδοσης δεν θα διατηρείται σε τόσο υψηλό νούμερο συνεχώς. Επιπλέον σε μια τέτοια κατάσταση ο αριθμός των νοσούντων θα είναι πολύ μεγάλος ενώ οι δυνητικά φορείς λιγότεροι με αποτέλεσμα να μην μπορεί να διατηρηθεί αυτός ο ρυθμός. Ωστόσο από το παράδειγμα αυτό δίνεται μια αίσθηση του πόσο ραγδαία μπορεί να εξελιχθεί το φαινόμενο της εξάπλωσης χωρίς εξωτερική παρέμβαση.
Μέθοδοι ελέγχου μιας επιδημίας
Για να ελεγχθεί μια επιδημία πρέπει ο ρυθμός με τον οποίο εμφανίζονται νέες περιπτώσεις ασθενών να είναι αρνητικός. Από το μοντέλο SIR υπολογίστηκε πως ο ρυθμός μεταβολής του πληθυσμού των ασθενών ή φορέων δίνεται από την εξίσωση
![]()
Για να έχουμε έλεγχο της επιδημίας και μείωση των ασθενών πρέπει να ισχύει η συνθήκη για την παραπάνω εξίσωση
![]()
ή ισοδύναμα
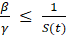
Ορίζουμε ως το βασικό αριθμό αναπαραγωγής της ασθένειας τον αριθμό
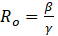
Από την παραπάνω σχέση ισχύει πως αν Ro > 1 τότε έχουμε έξαρση της επιδημίας, αν Ro < 1 έχουμε ύφεση ή απόσβεση ενώ αν Ro = 1 έχουμε εξισορρόπηση της επιδημίας σε σταθερή κατάσταση.
Από τα παραπάνω προκύπτει πως οι συντελεστές β, γ αποτελούν τους ποιοτικούς δείκτες ελέγχου μιας επιδημίας. Οι δείκτες αυτοί δεν είναι εύκολο να ελεγχθούν καθώς απαιτούνται συμβιβασμοί εκ μέρους του κράτους και της κοινωνίας.
Ο δείκτης μεταδοτικότητας β, που εκφράζει τον ρυθμό αύξησης των ασθενών σε σχέση με τους δυνητικά ασθενείς, επιθυμούμε να είναι όσο το δυνατόν μικρότερος. Αυτό επιτυγχάνεται λαμβάνοντας μέτρα αποκλεισμού με σημαντικό κόστος για την κοινωνία και την οικονομία τόσο άμεσα όσο και μεσοπρόθεσμα αλλά και με μέτρα απομόνωσης με σημαντικές επιπτώσεις στη σωματική και ψυχική υγεία των πολιτών (παιδεία, υγεία, ελευθερία).
Αντίθετα, ο δείκτης γ που εκφράζει την αύξηση της ίασης των ασθενών, επιθυμούμε να είναι όσο το δυνατόν μεγαλύτερος. Αυτό επιτυγχάνεται με την ενίσχυση του συστήματος υγείας που ωστόσο ενέχει αυξημένο κόστος για την πολιτεία. Ενισχύεται το σύστημα υγείας με την ανακάλυψη φαρμάκων για τη γρηγορότερη θεραπεία ασθενών και τη δημιουργία τεχνητής ανοσοποίησης μέσω εμβολιασμού, το οποίο και απαιτεί χρόνο και την εξάντληση των υλικών και ανθρώπινων πόρων του συστήματος υγείας.
Παράλληλα για τον έλεγχο των παραπάνω δεικτών εμφανίζονται και πολλές δυσκολίες που έχουν να κάνουν με τη φύση του προβλήματος. Τα δεδομένα δεν είναι πάντα αξιόπιστα και είναι δύσκολη η συλλογή τους έγκαιρα. Δεν υπάρχει επίσης αξιόπιστη μέθοδος που να δίνει μια ακριβή εκτίμηση για τους δείκτες β και γ, τέλος, υπάρχει διαφορά στη συμπεριφορά κάθε επιδημίας ανάλογα με το είδος και τη φύση της.
Ανοσία της αγέλης
Η ανοσία της αγέλης δημιουργείται, όταν πλέον έχει νοσήσει και θεραπευτεί το μεγαλύτερο ποσοστό του πληθυσμού. Αυτό συμβαίνει εξ’ αίτιας του γεγονότος πως, αν έχει θεραπευτεί ένα μεγάλο ποσοστό του πληθυσμού, η ασθένεια δεν μπορεί να βρει εύκολα δυνητικά ασθενείς (χωρίς αντισώματα) και να τους προσβάλλει. Πρακτικά είναι η τελευταία φάση μιας επιδημίας, όπως περιγράφεται στο λογιστικό μοντέλο στην οποία πλέον ο αριθμός των θεραπευθέντων είναι τόσο μεγάλος, που η ασθένεια δεν μπορεί να μεταδίδεται γρήγορα καθώς υπάρχει ανοσία στον πληθυσμό. Αυτό έχει σαν αποτέλεσμα να φθίνει σταδιακά η επιδημία. Μαθηματικά περιγράφεται από την εξίσωση:
![]()
Στην ασθένεια SARS-Cov-2 που ο ρυθμός μετάδοσης είναι Ro ≈ 3 υπολογίζουμε πως για να επιτευχθεί η ανοσία της αγέλης χρειάζεται ο πληθυσμός των δυνητικά ασθενών (αυτοί δηλαδή που δεν έχουν νοσήσει ή θεραπευτεί) να είναι μικρότερος του 1/3 του συνολικού πληθυσμού. Αυτό σημαίνει πως για την Ελλάδα τουλάχιστον ανοσία της αγέλης θα μπορούσε να επιτευχθεί αν είχαν νοσήσει τα 2/3 του πληθυσμού ήτοι περίπου 6,7 εκατομμύρια άνθρωποι.
Αυτή η προσέγγιση, ενώ δεν απαιτεί συμβιβασμούς, όπως παραπάνω, είναι ιδιαίτερα καταστροφική καθώς ως τότε θα έχει συσσωρευθεί ένας σημαντικός αριθμός ασθενών και πιθανώς νεκρών και προϋποθέτει πως ο ανθρώπινος οργανισμός αποκτά ανοσία για μεγάλο χρονικό διάστημα, πράγμα το οποίο δεν είναι πάντοτε βέβαιο.
Τέλος, η ανοσία της αγέλης μπορεί να επιτευχθεί και τεχνητά μέσω εμβολιασμού του πληθυσμού. Ο εμβολιασμός ουσιαστικά μετατρέπει έναν δυνητικά ασθενή σε θεραπευμένο προφέροντάς του τεχνητή ανοσία. Έτσι δε χρειάζεται να νοσήσει, και ενδεχομένως κατά συνέπεια να κινδυνεύσει, ώστε να αποκτήσει φυσική ανοσία.
Επίλογος
Η μελέτη και ο έλεγχος των πληθυσμών αποτελούσαν ανέκαθεν αντικείμενο μελέτης των επιστημόνων. Εδώ και πολλά χρόνια ο έλεγχος των μικροοργανισμών μας εξασφαλίζει τροφή, καθαριότητα και μια σειρά από άλλες βιομηχανικές εφαρμογές που βελτιώνουν τη ζωή μας. Σήμερα ωστόσο η θεωρία αυτή παίζει και έναν ακόμα σημαντικότερο ρόλο. Δίνει τη δυνατότητα στην επιστημονική κοινότητα να μπορεί να εκφράζει ποσοτικά και να προβλέπει την εξέλιξη μιας επιδημίας και να προτείνει τρόπους δράσης για την προστασία όλων, γεγονός πολύ σπουδαίο στις μέρες μας.
Πηγές
- Λυμπέρη Αναστασία. Μαθηματική μοντελοποίηση της εξάπλωσης μιας επιδημίας. Μεταπτυχιακή εργασία. Τμήμα Μαθηματικών Πανεπιστημίου Πατρών.
- A.Tsoularis (2001). Analysis of Logistic Growth Models Math. Sci 2, 23-46
- Hassan Khalil. Nonlinear Systems. ISBN-13: 978-0130673893
- Παγκόσμιος Οργανισμός Υγείας
Ηλ. Ταχ.: [email protected]
Ευθύμης Κυρίκος
Ηλεκτρολόγος Μηχανικός Ειδικός Αυτοματισμού και Ρομποτική

































































